Econ 57
Gary Smith
Fall 2009
Midterm Answers
1.
a. Scatter diagram.
b. Scatter diagram.
c. Boxplot.
d. Time series.
e. Scatter diagram.
2.
Higher Mean |
Higher Median |
Higher Standard Deviation |
|
| Case 1 | same |
same |
same |
| Case 2 | B |
same |
B |
| Case 3 | same |
same |
B |
| Case 4 | B |
B |
same |
3.
a. Women may be less likely to marry and more likely to divorce men who are in poor health.
b. Maybe men who don’t marry are in bad health to begin with. Maybe men who marry and have their health deteriorate the most get divorced.
c. For a controlled experiment, we could allow a random sample of men to marry and a random sample of married men to divorce.
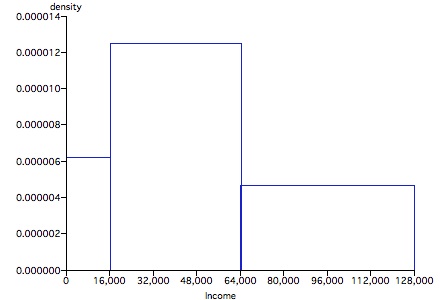
4. Collecting data:
| Taxable Income Bracket | Observations | Frequency | Frequency/Interval Width |
| $0 to $16,000 | 1 |
0.1 |
0.1/16,000 |
| $16,000 to $64,000 | 6 |
0.6 |
0.6/(64,000 - 16,000) = 0.2/16,000 |
| $64,000 to $128,000 | 3 |
0.3 |
0.3/(128,000 - 64,000) = 0.075/16,000 |
| $128,000 to $208,000 | 0 |
||
| $208,000 to $350,000 | 0 |
||
| $350,000 to no limit | 0 |
||
| Total | 10 |
1.0 |

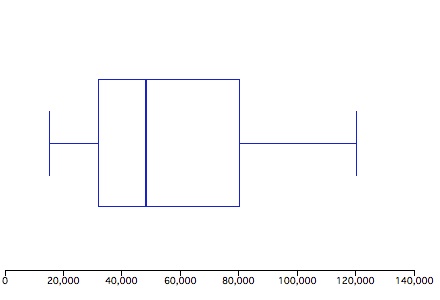
5. The minimum is $15,000; the maximum is $120,000; the median is $48,000; the first quartile is $32,000; and the third quartile is $80,000. Here is a box plot:
6.
a. This is a binomial problem with π = 0.1, n = 8, and x ≥ 3:
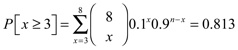
b. The probability of at least one lucky dollar among 4 dollar bills is equal to 1 minus the probability of no lucky dollars:1 - (1 - 0.813)^4 = 0.999
7. Using Bayes Rule,

Using a contingency table with 100,000 women:
++ |
not ++ |
Total |
|
| malignant | 1,000*0.8*0.8 = 640 |
1,000 - 640 = 360 |
1,000 |
| benign | 99,000*0.1*0.1 = 990 |
99,000 - 990 = 98,010 |
99,000 |
| Total | 1,630 |
98,370 |
100,000 |
The probability that a woman who gets two positive readings has a malignant lump is 640/1,630 = 0.3926.
8. The probabilities are
Number of Dice |
Probability |
0 |
(5/6)(5/6)(5/6) = 0.5787 |
1 |
3(1/6)(5/6)(5/6) = 0.3472 |
2 |
3(1/6)(1/6)(5/6) = 0.0694 |
3 |
(1/6)(1/6)(1/6) = 0.0046 |
Total |
1.0000 |
The expected value of the payoff is about an 8 percent loss per dollar wagered: 0(0.5787) + 2(0.3472) + 3(0.0694) + 4(0.0046) = 0.921.
9.
a. The probability that the 6 numbers chosen on Sept 10 will be the same 6 numbers chosen on Sept 6 (not necessarily in the same order) is equal to the probability that the 6 numbers chosen on Sept 10 will be any pre-specified 6 numbers:
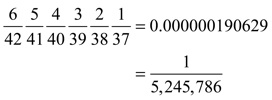
b. For an event with probability P, the expected wait until it happens is 1/P. Here, after the first lottery there is a probability P = 1/(5,245,787) probability that any lottery will match the previous one. So, the expected wait is 1 + 1/P = 5,245,787.
10.
a. (ii) because her Z value is Z = (70 - 66)/2 = 2 and the absolute value of his Z-value is less than 2: Z = (66 - 70)/2.5.
b. (i) because A is more likely than A and B, unless B is certain.
c. (ii) because A or B is more likely than A, unless B is impossible.
c. (ii) because is (i) is only one of the many ways that (ii) could be true. Think of it this way: (ii) is (i) and her height is more than 66 inches, and we know that A is more likely than A and B, unless B is certain.